OJ每日练习（16）

Posted on | In

题目名称

  1. Binary Tree Preorder Traversal（Leetcode #144）
  2. Binary Tree Inorder Traversal（Leetcode #94）
  3. Binary Tree Postorder Traversal（Leetcode #145）
  4. Binary Tree Level Order Traversal（Leetcode #102）
  5. Binary Tree Zigzag Order Traversal（Leetcode #103）
  6. Recover Binary Search Tree (Leetcode #99)
  7. Same Tree (Leetcode #100)
  8. Balanced Binary Tree (Leetcode #110)
  9. Flatten Binary Tree to Linked List（Leetcode #114）
  10. Populating Next Right Pointers in Each NodeⅡ (Leetcode #117）

Binary Tree Preorder Traversal（Leetcode #144）

解题思路

二叉树的几种遍历中，以后序最繁琐，前序中序都可以借助栈实现，但这里我将介绍Morris遍历，针对三种遍历次序，无需使用额外空间。（这里就不讨论递归了）
Morris遍历的前序和中序都较为简单，仅有后序较为繁琐。前序和中序的区别不大，因此将在中序遍历中统一说明。这里需要说明的是，前序和中序的区别是：

  • 前序
    若pre->right尚未线索化，输出当前序列，更新cur与pre。
  • 中序
    若pre->right已线索化，输出当前序列，更新cur与pre。

解题方案

栈（先进后出，所以先放右子）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        if(!root)
            return vector<int>();
        vector<int> res;
        stack<TreeNode*> stk;
        stk.push(root);
        while(!stk.empty()){
            TreeNode* temp = stk.top();
            stk.pop();
            res.push_back(temp->val);
            if(temp->right) stk.push(temp->right);
            if(temp->left) stk.push(temp->left);
        }
        return res;
    }
};

Morris

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        TreeNode* cur=root,*pre=nullptr;
        while(cur){
            if(!cur->left){
                res.push_back(cur->val);
                cur=cur->right;
            }
            else{
                pre=cur->left;
                while(pre->right && pre->right!=cur)
                    pre=pre->right;
                if(!pre->right){
                    res.push_back(cur->val);
                    pre->right=cur;
                    pre=cur;
                    cur=cur->left;
                }
                else{
                    pre->right=nullptr;
                    cur=cur->right;
                }
            }
        }
        return res;
    }
};

Binary Tree Inorder Traversal（Leetcode #94）

解题思路

Morris其算法核心思想在于线索华二叉树，具体步骤为：

  1. 如果当前节点的左孩子为空，则输出当前节点并将其右孩子作为当前节点。
  2. 如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。
      a) 如果前驱节点的右孩子为空，将它的右孩子设置为当前节点。当前节点(Cur)更新为当前节点的左孩子。
      b) 如果前驱节点的右孩子为当前节点（已经访问过），将它的右孩子重新设为空（恢复树的形状）。输出当前节点。当前节点更新为当前节点的右孩子。
  3. 重复以上1、2直到当前节点（Cur）为空。

以下为Morris中序遍历图：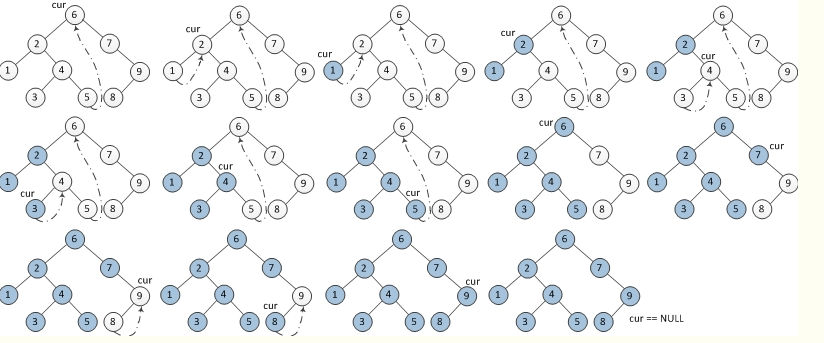
image_1cl377p8j1ubf2ecgi8bd21uen19.png-136.1kB

解题方案

栈(一直向左，直至五路可走转向右）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> stk;
        while(true){
            if(root){
                stk.push(root);
                root=root->left;
            }
            else if(stk.empty()) break;
            else{
                root =stk.top();
                stk.pop();
                res.push_back(root->val);
                root=root->right;
            }
        }
        return res;
    }
};

Morris

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        TreeNode* cur=root,*pre=nullptr;
        while(cur){
            if(!cur->left){
                res.push_back(cur->val);
                cur=cur->right;
            }
            else{
                pre=cur->left;
                while(pre->right && pre->right!=cur)
                    pre=pre->right;
                if(pre->right==cur){
                    res.push_back(cur->val);
                    pre->right=nullptr;
                    pre=cur;
                    cur=cur->right;
                }
                else{
                    pre->right=cur;
                    cur=cur->left;
                }
            }
        }
        return res;
    }
};

Binary Tree Postorder Traversal（Leetcode #145）

解题思路

后序遍历的难度远大于前序与中序，这里将给出stack与morris的实现。

解题方案

栈（借助stack还需要cur与pre）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> stk;
        TreeNode* cur=root,*pre=nullptr;
        while(cur || !stk.empty()){
            if(cur){
                stk.push(cur);
                cur=cur->left;
            }
            else{
                TreeNode* top = stk.top();
                if(top->right==pre || top->right==nullptr){
                    // has no right child or right child has been visited
                    res.push_back(top->val);
                    pre=top;
                    stk.pop();
                }
                else
                    cur=top->right;
            }
        }
        return res;
    }
};

栈配合双端队列（反转前序的过程）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        if(!root)
            return vector<int>();
        stack<TreeNode*> stk;
        deque<int> res;
        stk.push(root);
        while(!stk.empty()){
            TreeNode* top = stk.top();
            stk.pop();
            res.push_front(top->val);
            if(top->left) stk.push(top->left);
            if(top->right) stk.push(top->right);
        }
        return vector<int>(res.cbegin(),res.cend());
    }
};

morris

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        TreeNode dummy(-1);
        TreeNode *cur, *pre = nullptr;
        function<void (TreeNode*)> visit = [&res](TreeNode* node) {res.push_back(node->val); };
        dummy.left = root; cur = &dummy;
        while (cur) {
            if (!cur->left) {
                pre = cur;
                cur = cur->right;
            }
            else {
                TreeNode *node = cur->left;
                while (node->right && node->right != cur) {
                    node = node->right;
                }
                if (!node->right) {
                    node->right = cur;
                    pre = cur;
                    cur = cur->left;
                }
                else {
                    visit_reverse(cur->left, prev, visit);
                    prev->right = nullptr;
                    prev = cur;
                    cur = cur->right;
                }
            }
        }
        return res;
    }
private:
    void reverse(TreeNode* from, TreeNode* to) {
        TreeNode* x = from, *y = from->right, *z;
        if (from == to) return;
        while (x != to) {
            z = y->right;
            y->right = x;
            x = y;
            y = z;
        }
    }
    void visit_reverse(TreeNode* from, TreeNode* to, function<void (TreeNode*)> &visit) {
        TreeNode* p = to;
        reverse(from, to);
        while (true) {
            visit(p);
            if (p == from) break;
            p = p->right;
        }
        reverse(to, from);
    }
};

Binary Tree Level Order Traversal（Leetcode #102）

解题思路

如果仅输出一个vector，层序遍历和前序遍历几乎一致，只需要把stack换成queue。如果需要输出vector<vector<vector<int> >,则递归的思路写起来十分清晰。此外，也可以使用两个queue来解决问题。

解题方案

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int> > res;
        aux(root,1,res);
        return res;
    }
private:
    void aux(TreeNode* root,size_t level,vector<vector<int> >& res){
        if(!root)
            return;
        if(level>res.size())
            res.push_back(vector<int>());
        res[level-1].push_back(root->val);
        aux(root->left,level+1,res);
        aux(root->right,level+1,res);
    }
};

双queue

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        deque<TreeNode*> current,next;
        vector<vector<int> > res;
        if (!root) return res;
        vector<int> level;
        current.push_back(root);
        while (!current.empty()){
            while(!current.empty()){
                root = current.front();
                current.pop_front();
                level.push_back(root->val);
                if (root->left) next.push_back(root->left);
                if (root->right) next.push_back(root->right);
            }
            res.push_back(level);
            level.clear();
            swap(next, current);
        }
        return res;
        }
};

扩展（ Binary Tree Level Order Traversal II Leetocde107）

题目描述

Given a binary tree, return the bottom-up level order traversal of its nodes’ values. (ie, from left to right, level by level from leaf to root).
For example:

1
2
3
4
5
6
7
8
9
10
11
12
Given binary tree [3,9,20,null,null,15,7],
    3
   / \
  9  20
    /  \
   15   7
return its bottom-up level order traversal as:
[
  [15,7],
  [9,20],
  [3]
]

解题思路

如果要偷懒的话，直接reverse上一题的答案即可，但我辈当然不齿这种方案。那只能先获取整个树的高度，然后对于指定的位置的vector执行push_back，总得来说问题不大。

解题方案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        int size = height(root);
        if(size==0) return vector<vector<int> >();
        vector<vector<int> > res(size);
        aux(root,1,res);
        return res;
    }
private:
    int height(TreeNode* root){
        if(!root) return 0;
        return max(height(root->left),height(root->right))+1;
    }
    void aux(TreeNode* root,int level,vector<vector<int> >& res){
        if(!root) return;
        res[res.size()-level].push_back(root->val);
        aux(root->left,level+1,res);
        aux(root->right,level+1,res);
    }
};

Binary Tree Zigzag Order Traversal（Leetcode #103）

解题思路

这道题的思路和上一题类似，但是遇到奇数层就push_back，遇到偶数层就push_front即可。但对于vector来说，在头端插入需要线性的时间，因此需要别的数据结构并加以转化，此题也许用迭代效果更佳。（利用stack实现倒序）

解题方案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
       	vector<vector<int> > res;
	    if (!root) return res;
	    deque<TreeNode*> dtn;
	    dtn.push_back(root);
	    bool leftToRight = true;
	    while (!dtn.empty()) {
		    int size = dtn.size();
		    vector<int> row(size);
		    for (int i = 0; i < size; i++) {
			    TreeNode* node = dtn.front();
			    dtn.pop_front();
			    // find position to fill node's value
			    int index = (leftToRight) ? i : (size - 1 - i);
			    row[index] = node->val;
			    if (node->left) dtn.push_back(node->left);
			    if (node->right) dtn.push_back(node->right);
		    }
		    //after this level
		    leftToRight = !leftToRight;
		    res.push_back(row);
	    }
	    return res;
    }
};

Recover Binary Search Tree (Leetcode #99)

题目描述

Two elements of a binary search tree (BST) are swapped by mistake.Recover the tree without changing its structure.
Example1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Input: [1,3,null,null,2]

   1
  /
 3
  \
   2

Output: [3,1,null,null,2]

   3
  /
 1
  \
   2

Example2:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Input: [3,1,4,null,null,2]

  3
 / \
1   4
   /
  2

Output: [2,1,4,null,null,3]

  2
 / \
1   4
   /
  3

解题思路

中序遍历将其存在一个vector中，通过查看逆序对就能明确哪两个需要交换。如果不能使用辅助存储空间，则需要借助morris遍历实现。

此外，该问题亦存在递归解法，采用pre与first、second三个指针记录中序遍历下的逆序对。若存在逆序对，若first尚不明确，将pre赋予first（乱序的两个节点在中序下相邻），再将root赋予sec。

解题方案

空间O(n)的中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    void recoverTree(TreeNode* root) {
        vector<TreeNode*> store;
        inOrderTraverse(root, store);
        swapValue(store);
    }
private:
    void inOrderTraverse(TreeNode* &root, vector<TreeNode*> &res) {
        if (!root) return;
        if (root->left) inOrderTraverse(root->left, res);
        res.push_back(root);
        if (root->right) inOrderTraverse(root->right, res);
    }
    void swapValue(vector<TreeNode*> &vtn) {
        if (vtn.empty() || vtn.size() == 1) return;
        for (size_t i = 0; i != vtn.size(); ++i) {
            for (size_t j = 0; j != vtn.size() - i - 1; ++j) {
                if (vtn[j]->val > vtn[j + 1]->val) swap(vtn[j]->val, vtn[j + 1]->val);
            }
        }
    }
};

递归（DFS）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    void recoverTree(TreeNode* root) {
        TreeNode* pre=nullptr,*first=pre,*sec=pre;
        aux(root,pre,first,sec);
        if(first && sec) swap(first->val,sec->val);
    }
private:
    void aux(TreeNode* root,TreeNode* &pre,TreeNode* &first,TreeNode* &sec ){
        if(!root) return;
        aux(root->left,pre,first,sec);
        if(pre && pre->val>root->val){
            if(!first) first=pre;
            sec=root;
        }
        pre=root;
        aux(root->right,pre,first,sec);
    }
};

Morris中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
public:
    void recoverTree(TreeNode* root) {
        pair<TreeNode*, TreeNode*> broken;
        TreeNode* prev = nullptr;
        TreeNode* curr = root;
        while (curr){
            if (!curr->left) {
                detect(broken, prev, curr);
                prev = curr;
                curr = curr->right;
            }
            else {
                auto node = curr->left;
                while (node->right && node->right!=curr){
                    node = node->right;
                }
                if (!node->right) {
                    node->right = curr;
                    curr = curr->left;
                }
                else{
                    detect(broken, prev, curr);
                    node->right = nullptr;
                    prev = curr;
                    curr = curr->right;
                }
            }
        }
        swap(broken.first->val, broken.second->val);
    }
private:
    void detect(pair<TreeNode*, TreeNode*> &broken, TreeNode* prev, TreeNode* curr) {
        if (prev && prev->val > curr->val) {
            if (!broken.first) broken.first = prev;
            broken.second = curr;
        }
    }
};

Same Tree (Leetcode #100)

解题思路

这道题可以引申出子树问题（剑指offer已经解答），值得留意。

解题方案

1
2
3
4
5
6
7
8
9
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(!p && !q) return true;
        if(!p || !q) return false;
        if(p->val!=q->val) return false;
        return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
    }
};

扩展（Symmetric Tree Leetcode #101)

解题方案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if(!root)
            return true;
        return aux(root->left,root->right);
    }
private:
    bool aux(TreeNode* left,TreeNode* right){
        if(!left && !right) return true;
        if(!left || !right) return false;
        if(left->val!=right->val) return false;
        return aux(left->left,right->right) && aux(left->right,right->left);
    }
};

扩展（Invert Binary Tree Leetcode #226）

解题思路

用递归的话十分容易，用迭代则需要一个queue作为辅助空间走一次BFS。

解题方案

递归

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root){
            invertTree(root->left);
            invertTree(root->right);
            std::swap(root->left,root->right);
        }
        return root;
    }
};

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        queue<TreeNode*> q;
        q.push(root);
        while(!q.empty()){
            TreeNode* temp=q.front();
            q.pop();
            if(temp){
                q.push(temp->left);
                q.push(temp->right);
                swap(temp->left,temp->right);
            }
        }
        return root;
    }
};

Balanced Binary Tree (Leetcode #110)

解题思路

注意剪枝

解题方案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        return deepth(root)>=0;
    }
private:
    int deepth(TreeNode* root){
        if(!root)
            return 0;
        int left = deepth(root->left);
        int right = deepth(root->right);
        if( left < 0 || right < 0 || abs(left-right)>1) 
            return -1;
        return max(left,right)+1;
    }
};

Flatten Binary Tree to Linked List（Leetcode #114）

题目描述

Given a binary tree, flatten it to a linked list in-place.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
For example, given the following tree:
    1
   / \
  2   5
 / \   \
3   4   6
The flattened tree should look like:
1
 \
  2
   \
    3
     \
      4
       \
        5
         \
          6

解题思路

既然要求就地，那只能寻找规律了。可以设立cur表征当前节点，当cur==nullptr时终止循环。若其左右子树健全，寻找其中序遍历下的pre，令pre->right=cur->right。接着将右子树绑定到左子树cur->right=cur->left。最后切断左子树与根的联系，转向右子树。

解题方案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    void flatten(TreeNode* root) {
        TreeNode* cur=root;
        while(cur){
            if(cur->left && cur->right){
                TreeNode* pre = cur->left;
                while(pre->right) pre=pre->right;
                pre->right=cur->right;
            }
            if(cur->left)
                cur->right=cur->left;
            cur->left=nullptr;
            cur=cur->right;
        }
    }
};

Populating Next Right Pointers in Each NodeⅡ (Leetcode #117）

题目描述

Given a binary tree

1
2
3
4
5
struct TreeLinkNode {
  TreeLinkNode *left;
  TreeLinkNode *right;
  TreeLinkNode *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Note:
You may only use constant extra space.
Recursive approach is fine, implicit stack space does not count as extra space for this problem.
Example:
1
2
3
4
5
6
7
8
9
10
11
12
Given the following binary tree,
     1
   /  \
  2    3
 / \    \
4   5    7
After calling your function, the tree should look like:
     1 -> NULL
   /  \
  2 -> 3 -> NULL
 / \    \
4-> 5 -> 7 -> NULL

解题思路

由于需要常量空间,BFS不可行，因此只能再次通过设立cur，head，tail的方案，逐层地扫描建立。算法核心思想为：head与tail分别表征下一层的起点与重点（横向），若cur存在左子，若tail存在则更新tail，否则初始化tail与head。存在右子时亦是如此。cur左右子扫描完毕后cur=cur->next。若其为空，则令cur转向下一层头部，并将tail与head置零。

如果去除常量空间这个条件，那么BFS算法如下所示。

解题方案（优解）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    void connect(TreeLinkNode *root) {
        TreeLinkNode* cur=root,*head=nullptr,*tail=nullptr;
        while(cur){
            if(cur->left){
                if(tail){
                    tail->next=cur->left;
                    tail=tail->next;
                }
                else{
                    tail=cur->left;
                    head=tail;
                }
            }
            if(cur->right){
               if(tail){
                    tail->next=cur->right;
                    tail=tail->next;
                }
                else{
                    tail=cur->right;
                    head=tail;
                }
            }
            cur=cur->next;
            if(!cur){
                cur=head;
                head=tail=nullptr;
            }
        }
    }
};

解题方案（BFS）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    void connect(TreeLinkNode *root) {
        if(!root) return;
        queue<TreeLinkNode*> q;
        q.push(root);
        while(!q.empty()){
            int size = q.size();
            while(size--){
                root=q.front();
                q.pop();
                if(size) root->next=q.front();
                else root->next=nullptr;
                if(root->left) q.push(root->left);
                if(root->right) q.push(root->right);
            }
        }
    }
};