OJ每日练习（4）

Posted on | In

题目名称

  1. Two Sum（Leetcode #1)
  2. 3Sum(Leetcode #15）
  3. 3Sum Closet(Leetcode #16)
  4. 用两个栈实现队列（剑指offer #9）
  5. 斐波那契数列（剑指offer #10）
  6. 旋转数组的最小数字(剑指offer #11)

Two Sum（Leetcode #1)

题目描述

Given an array of integers, return indices of the two numbers such that they add up to a specific target.You may assume that each input would have exactly one solution, and you may not use the same element twice.
Example:

1
2
3
Given nums = [2, 7, 11, 15], target = 9,
Because nums[0] + nums[1] = 2 + 7 = 9,
return [0, 1].

解题思路

  1. 暴力查找，O(n^2),不可取。
  2. hash_table，占用空间
  3. 排序，然后左右夹逼。但leetcode要求返回的是数组下标，此法不可行。剑指offer上有一道可用此法解决。

解题方案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> twoSum(vector<int> &numbers, int target){
	    unordered_map<int, int> hash;
	    vector<int> res;
	    for (int i = 0; i < numbers.size(); i++) {
		    int numberToFind = target - numbers[i];
		    if (hash.find(numberToFind) != hash.end()) {
			    res.push_back(hash[numberToFind]);
			    res.push_back(i);			
			    return res;
		    }
		    hash[numbers[i]] = i;
	    }
	    return res;
    }
};

(一开始以为这道题并不麻烦，结果忽略了数组元素可能重复的事实，吃了大亏。在存入hashtable时应当注意不可直接全部存入，而是遍历式地存取）

扩展

顺手用夹逼解决剑指offer#57，它的题目描述如下所示：输入一个递增排序的数组和一个数字S，在数组中查找两个数，使得他们的和正好是S，如果有多对数字的和等于S，输出两个数的乘积最小的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    vector<int> FindNumbersWithSum(vector<int> array,int sum) {
        auto i=array.cbegin();
        auto j=array.cend();
        if(i==j||i==--j)
            return vector<int>();
        vector<int> res;
        while(i!=j){
            if(*i+*j==sum){
                res.push_back(*i);
                res.push_back(*j);
                return res;
            }
            else if(*i+*j<sum)
                ++i;
            else
                --j;
        }
        return res;
    }
};

3Sum(Leetcode #15）

题目描述

Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0?Find all unique triplets in the array which gives the sum of zero.
Note:
The solution set must not contain duplicate triplets.
Example:

1
2
3
4
5
6
Given array nums = [-1, 0, 1, 2, -1, -4],
A solution set is:
[
  [-1, 0, 1],
  [-1, -1, 2]
]

解题思路

这道题的思路还是排序，然后运用双指针夹逼。首先定义一个指针i指向首节点，然后在其后序元素中不断查找sum=-*i的节点对。待i查找完毕后，向后推进。当*i+*(i+1)+*(i+2)大于0时，结束遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        auto i = nums.cbegin();
        if(nums.size()<3 || *i>0)
            return vector<vector<int> >();
        set<vector<int> > res;// make result unique
        while(i!=nums.cend()-2 && (*i+*(i+1)+*(i+2)<=0)){          
            auto j = i+1;
            auto k = nums.cend()-1;
            while(j!=k){
                if((*j+*k)== -*i){
                    vector<int> curres;
                    curres.push_back(*i);
                    curres.push_back(*j);
                    curres.push_back(*k);
                    res.insert(curres);
                    ++j;
                }
                else if((*j+*k)<-*i)
                    ++j;
                else
                    --k;
            }
            ++i;
        }
        return vector<vector<int> >(res.cbegin(),res.cend());
    }
};

扩展

在此思路上读者不难想到，求解KSUM的思路均是一致的：先排序，后夹逼即可，因此本文不再收录4SUM的解法。

3Sum Closet(Leetcode #16)

题目描述

Given an array nums of n integers and an integer target, find three integers in nums such that the sum is closest to target. Return the sum of the three integers. You may assume that each input would have exactly one solution.
Example:

1
2
Given array nums = [-1, 2, 1, -4], and target = 1.
The sum that is closest to the target is 2. (-1 + 2 + 1 = 2).

解题思路

本题的思路与上一题几乎完全一致，只是细节不同。本题中可以设定一个全局变量以保存与target的最小差值，最后返回target与该差值之和即可，当然，若发现最优差值为0，直接返回target。

解题方案

（偷了一下懒，拿出了之前写的code，粗略看了一下应该可以优化，例如在当前abs(dis)大于abs(mindis)且继续增加时直接退出本轮循环）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int threeSumClosest(vector<int>& nums, int target) {
        if (nums.size() <= 3) 
            return accumulate(nums.cbegin(), nums.cend(), 0);
	    sort(nums.begin(), nums.end());
	    int mindis = numeric_limits<int>::max();
	    for (int index = 0; index != nums.size() - 2; ++index) {
		    int aim = target - nums[index];
		    int start = index + 1, end = nums.size() - 1;
		    while (start < end) {
			    int sum = nums[start] + nums[end];
			    int dis = sum - aim;
			    mindis = abs(dis) < abs(mindis) ? dis : mindis;
			    if (dis==0)
                    return target;
			    else if (dis>0) 
                    --end;
			    else
				    ++start;
			}
		}
	    return target + mindis; 
    }
};

用两个栈实现队列（剑指offer #9）

解题思路

现有两个栈s1、s2,在执行push操作时总是将元素push入s1。在执行pop操作时，若当前s2非空，对s2执行pop操作，否则将s1中的所有元素push进入s2（两次先进后出变成了先进先出）。

解题方案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution{
public:
    void push(int node) {
        stack1.push(node);
    }

    int pop() {
        if(stack2.empty()){
            while(!stack1.empty()){
                int temp = stack1.top();
                stack2.push(temp);
                stack1.pop();
            }  
        }
        int res = stack2.top();
        stack2.pop();
        return res;
    }

private:
    stack<int> stack1;
    stack<int> stack2;
};

扩展

如何用队列实现一个栈？有两种策略，第一种策略需要两个队列，而第二种只需要一个队列。下文将依次讲解思路。

  1. 2个队列实现栈
    假定现有队列q1、q2,当执行push操作时总是push入q1。当执行pop操作时，若当前q1.size()>1,则将其元素全部push进入q2，然后再pop最末元素。最后，将swap(q1,q2)，令q2再次为空。当然，也可以每一次pop时检查哪个队列为空，将其作为中转，就不用在最后swap了。
  2. 1个队列实现栈
    原理很简单，每执行一次push就对queue作一次重排，保证queue的次序与stack一致。具体操作如下图所示：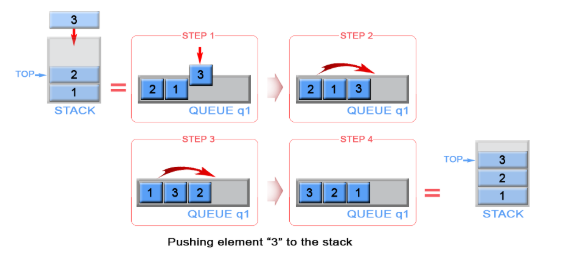
    image_1cjve99rd1p371d0v7h75lu1gff9.png-35.5kB

斐波那契数列（剑指offer #10）

解题思路

没什么好说的，值得注意的是类似爬楼梯之类问题本质也是求解斐波拉契数列。

解题方案

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int Fibonacci(int n) {
        if(n==0 || n==1) return n;
        int f=0,g=1;
        while(--n){
            g=f+g;
            f=g-f;
        }
        return g;
    }
};

旋转数组的最小数字(剑指offer #11)

解题思路

本题已经在OJ exercise2 http://xander.wiki/post/969534c9.html 中提到并实现了。下文将给出存在元素重复的情况。

解题方案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int minNumberInRotateArray(vector<int> rotateArray) {
        if(rotateArray.empty())
            return 0;
        else if(rotateArray.size()==1)
            return rotateArray[0];
        int lo=0;
        int hi=rotateArray.size()-1;
        while(lo<hi){
            int mid = lo+(hi-lo)/2;
            if(rotateArray[mid]<rotateArray[hi])
                hi=mid;
            else if(rotateArray[mid]==rotateArray[hi])
                --hi;
            else
                lo=mid+1;
        }
        return rotateArray[lo];
    }
};